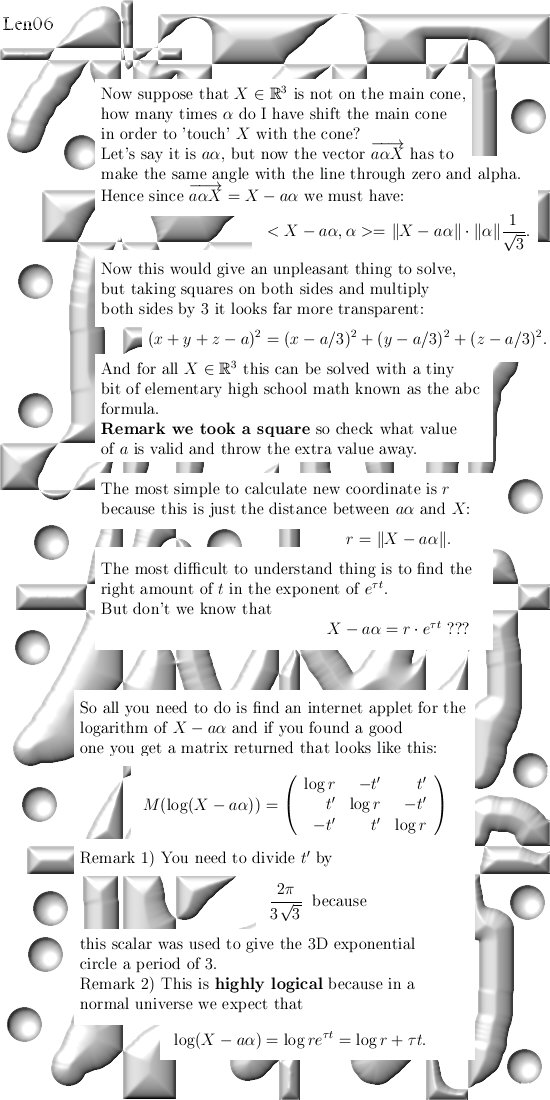|
A primer on the
three dimensional complex numbers.
|
| Introduction: This
file is a collection of the pictures from Feb 2012 until now that are
related to the 3D complex numbers. 3D complex numbers are in many ways just like the ordinary complex numbers from the complex plane; only in the 3D case you simply 'create' an 'imaginary number' j who's third power equals minus one. Recall that in the ordinary complex plane the 'imaginary unit' i has a square of minus one. Just like ordinary complex numbers (written often as z = x + iy) it looks rather elementary to use rectangular coordinates in real numbers (x, y, z). Therefore the number one is
written as 1 = (1, 0, 0) __________ So only pictures in this stuff below... Remark: Everywhere where in these pictures it says 'see below' you must read that as 'see above' in some other picture. (Because this file is chronological while the homepage of this website is anti-chronological.) |
|
|
|
|
| From 09
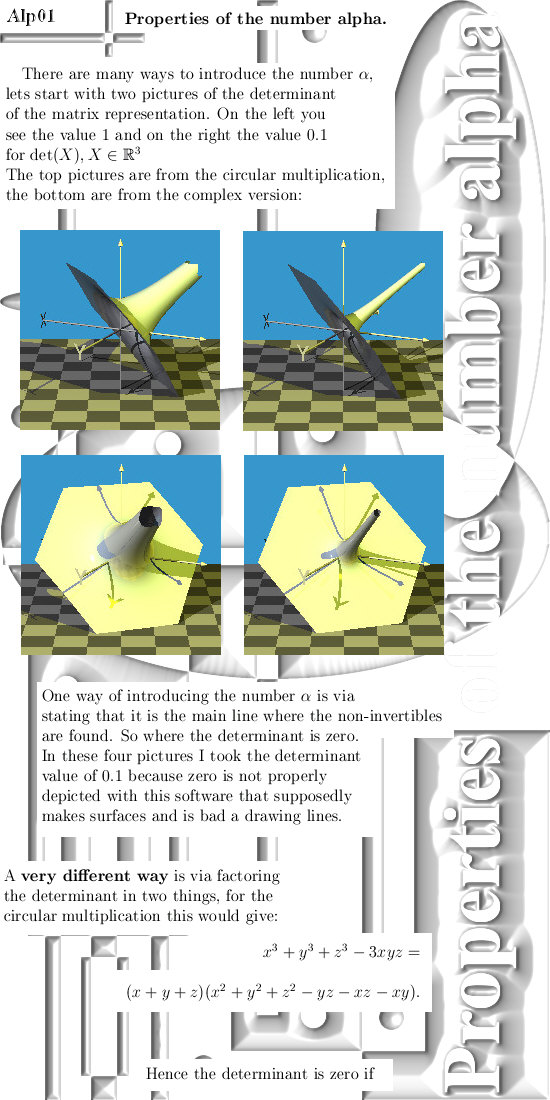
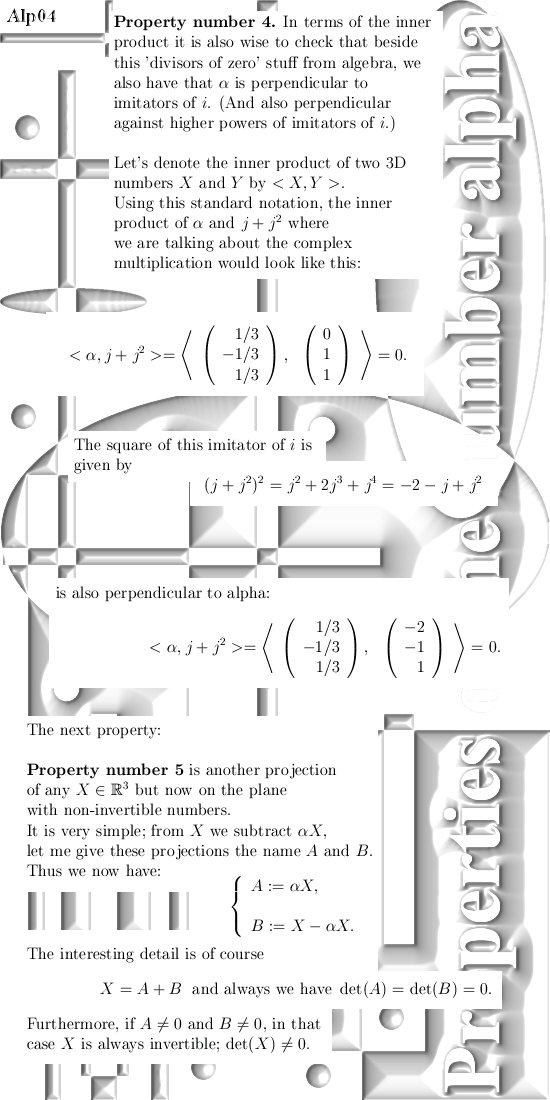
Feb 2016: Seven properties of the number alpha in 3D.
A few days back on the new website 3Dcomplexnumbers.net I said my next post would be about the elementary properties of the number alpha. Yet as I wrote it out it would become a bit too long for a post over there, it is about 5 A4 size pages. And since I did not post anything on this website, now it is February I thought: let's hang it in here.
So all in all there is nothing new
in here, but now all those elementary properties of the most important non-invertible
number alpha are grouped together. Furthermore I gave a few ways of
introducing this number.
|
|
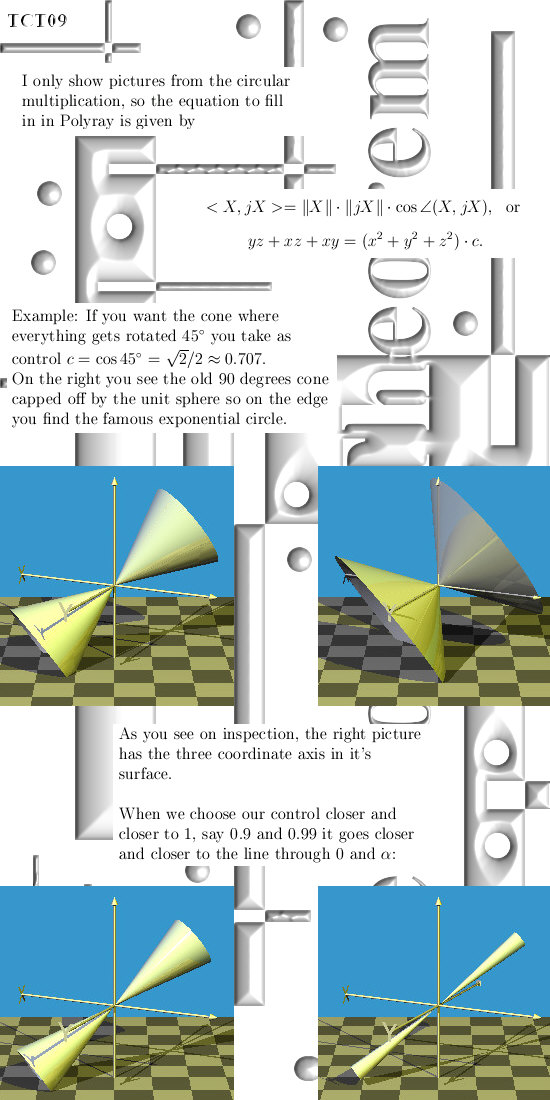
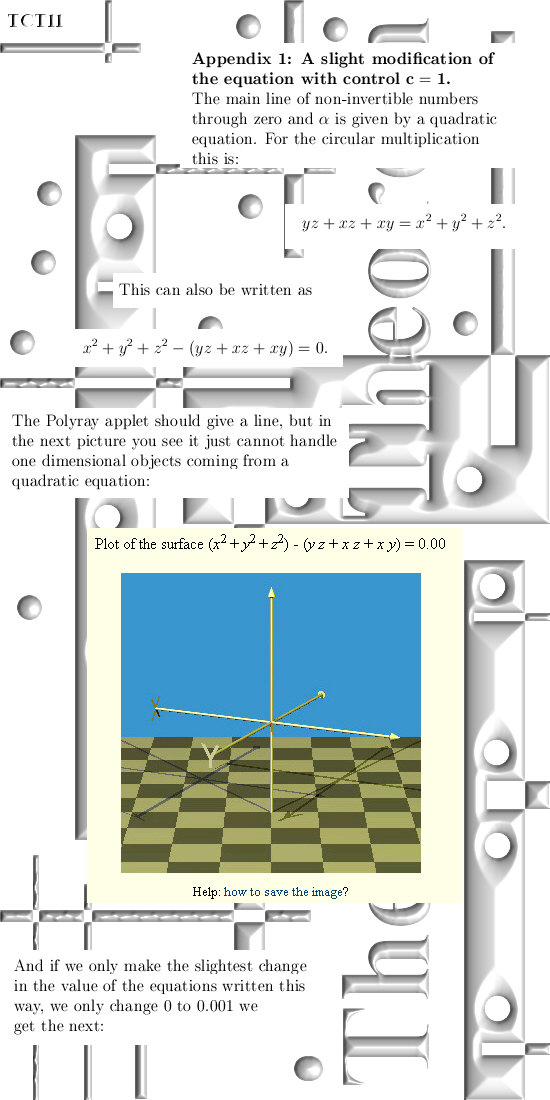
From 22
Feb 2016: The Cone Theorem.
In this update we take a look at
all subspaces of the 3D complex and circular numbers that are shifted by a
fixed angle if you multiply a 3D number X by an imaginary unit like j or
j^2. This update is 12 pages long.
Link to the Polyray applet: http://wims.math.leidenuniv.nl/wims/wims.cgi (likely you must search a little bit...) Till updates.
|
|
From 15 April
2016: Debunking the Euler evaluation of zeta at minus one.
Last Monday this week I was at a
public lecture given by a professional math professor named Frits Beukers. I
went there because I had some vague hopes that I could observe some serious
analytical continuation of the zeta function. Now in the science of physics they use it all the time: If they encounter 1 + 2 + 3 + 4 + 5 + etc they simply replace it by -1/12 and after that they think the problems are solved. By doing so the science of physics is turned into the pseudo science of physics; also every time you see one of those overpaid professional professors seriously talking about this -1/12 you are observing tax payer money burned for no reason at all. __________ In this update, only three pictures long, we are going to debunk this nonsense from Euler and other people. I do not blame Euler in any way, his record is clear and as far as I am concerned he is still standing at position number on of math people in the all time rankings... So I do not blame Euler that at present day we have all these idiots around using three or four brain cells and explaining that 1 + 2 + 3 + 4 + etc = -1/12. __________ Update from 20 April: I emailed Daughter
with a short version of the proof below and she told me she absolutely did
not understand one thing from it. That made me scratch my head because in
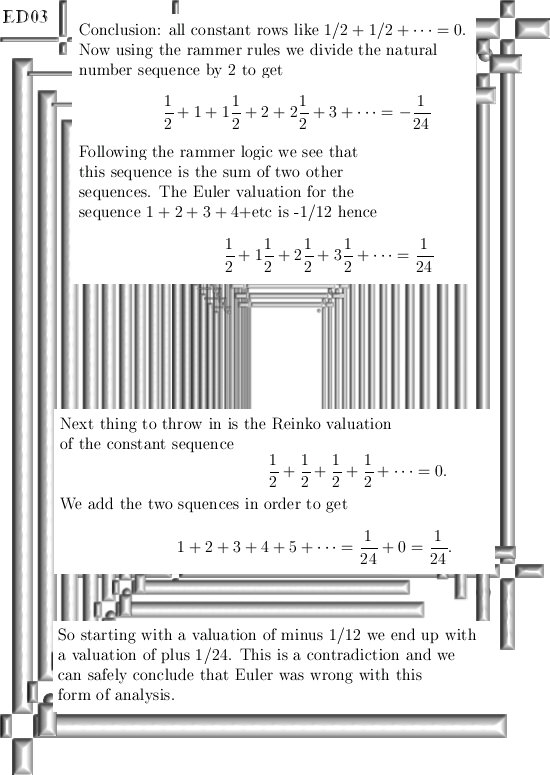
principle the proof below is not difficult at all. ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12 Here are the three pictures:
I could post many links to all
kinds of files that say 1 + 2 + 3 + 4 + 5 + etc = -1/12, but look for yourselves
if you want to see the brains of those idiots in action... Update from 21 Apr 2016: In the above three pictures I showed you a simple proof using very basic math and we first 'proved that' 1 + 1 + 1 + 1 + etc etc =0. And as such all constant arrays should be zero. But you can talk that stuff to any value, look we first take the sum of all natural numbers (and once more first pretend Euler was right so we valuate it): 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + etc etc = -1/12. Now all of a sudden from number 5 we raise everything with 1, so that gives: 1 + 2 + 3 + 4 + 6 + 7 + 8 + 9 + etc etc = ???
As you see on inspection: these are
all natural numbers except for the number 5.
If we stick to the valuation of the
constant array or row as 1 + 1 + 1 + etc = 0, in that case ??? = -5 1/12. Tiny problem: The last detail would imply 1 + 1 + 1 + 1 + etc = 5 because that is what has gone missing... Huge problem: We can repeat this line of reasoning for every natural number. Conclusion: Likely there is something wrong with the assumption that it should be -1/12 in the first place... Till updates. Update from 29 April 2016: For some strange reason there were suddenly much more Youtube video's out there on the crazy Euler evaluation of the zeta function at minus one. I will not post any link or so, likely if you read this you do a Youtube seach for yourself on for example 'The sum of all integers'. Two more pictures and that is definitely the very end of this update:
The best video out there also
debunking the Euler idea that 1 + 2 + 3 + etc = -1/12 was posted two years
back and here is the link and stuff: What
is a function? Why 1+2+3+4+5+.... not equals -1/12 = Zeta(-1) At last I want to remark that Euler is one of my heroes when it comes to math, so for myself speaking it was great fun to debunk a tiny bit of his insights. Till updates. __________ Added on 14 Jan 2018:
Finally the Mathologer guy is doing
the right thing and is also debunking this nonsense from the Nottingham
professors. He has a video of about 42 minutes where in detail he exposes
the dumb lines of reasoning as done by the Nottingham professors. At the end
of the video he also enters the realm of analytic continuation in order to
evaluate the zeta function at zeta = -1. This does not mean that 1 + 2 + 3 + 4 + 5 + ..... = -1/12. Here is the video:
Numberphile v. Math: the truth about 1+2+3+...=-1/12
Also do not forget to visit the new
website: 3Dcomplexnumbers.net Till updates.
|
|
From 06
May 2016 : On the length of the product of two 3D numbers.
The honorable Gauss had a motto stating 'Few but ripe' and with that he meant only a few publications but they had to be ripe. Likely this was caused by the fact that Gauss, just like me, has experienced very negative things when dealing with professional math people. And Gauss, just like me, thought you are better of if you avoid all contacts with these weirdo's for the rest of your life. Now I disagree with the Gauss motto, I like to write as much as I see fit but one thing will be very clear: Never in my life I will write a peer reviewed article, let it be in math or physics. I am really not waiting for the approval of some overpaid idiot commenting on my work. After all, the math professors have their stupid 2-4-8 theorem on higher dimensional numbers while the physics professors worship the electron that is supposedly to be a magnetic dipole. Idiots like that might be funny to look at just like a flock of monkeys on a rock is nice to look at, but just like I do not ask a chimpanzee if this kind of work might be worth publishing I do not ask any professional professor to do the same. __________ Ok, this update is about the length of AX when A and X are both circular 3D numbers. In the complex plane we have this preservation of length meaning that for two complex numbers from the complex plane we always have |az| = |a| |z| or to put it in words: The length of the product of two complex numbers is the product of the length's of both complex numbers. In three dimensions it is very different: We can have shrinkage, equality and extra growth. The equality stuff covers all thing related to 3D complex number use in quantum mechanics, so that is in the pocket. So all previous updates stay valid, let there be no worry. __________ This update is eight pictures long, sized 550 x 1100 pixels each. Have fun reading it.
For myself speaking I consider it a great honor to construct a completely new way of crafting a coordinate system. So beside the rectangular coordinates like the (x, y, z) notation, there are also 3D spherical coordinate systems and cylindrical coordinate systems. Now we also have this cone sweeping system and as usual my dear reader: Zero reaction from professional professors, let it be math or physics. __________ A day later I realized I
completely forget to give a link to the matrix log applet, here is a
nice set of over 40 matrix applets: If you did choose the wrong a in your [a, r, t] coordinates you get a matrix that makes no sense, so the method of finding the [a, r, t] coordinates is foolproof I guess...;) Let's leave it with that. Till updates.
|
|
From 06
Sept 2016: Systems of differential equations.
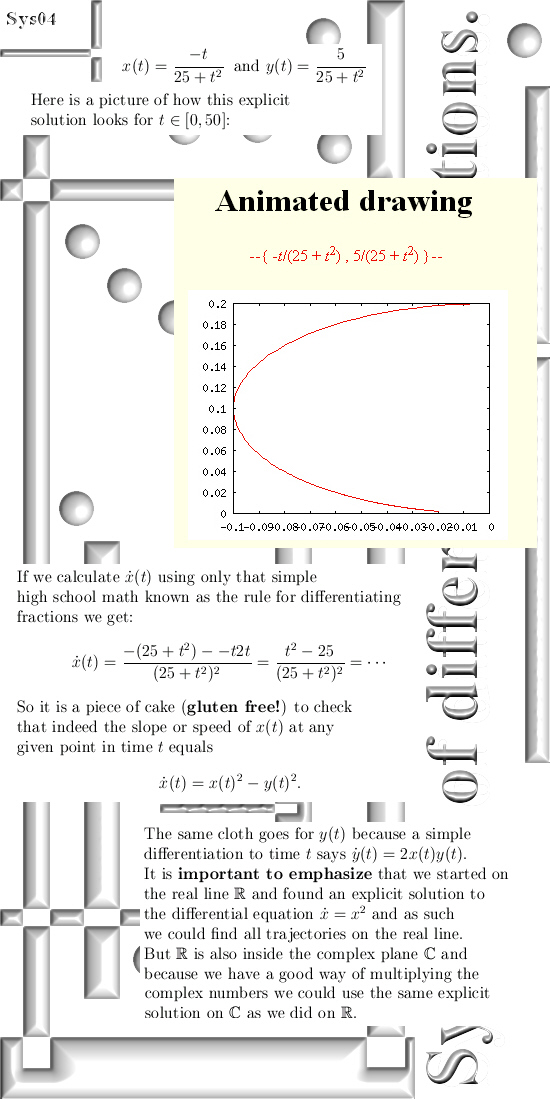
This update is about the time evolutions on complex and circular number systems, we start with a simple example from the real line: Find a function x(t) such that the speed equals x(t)^2 and we start with x(0) = 1/2 so the speed in x = 1/2 equals 1/4.
In Part 1 this simple example is
expanded to the complex plane and the three dimensional complex number
system. Old methods related to overpaid math professors who think that it is impossible to craft a 3D complex number system fail although I do not offer a mathematical proof for this. Just look at history: They have no methods to solve for systems of differential equations like this. Anyway I am not aware of they having this capability. In Part 1 it is more or less like: If you can solve the differential equation on the real line, you can try to expand it to higher dimensions. In Part 2 we focus on trying to find the Taylor coefficients in case you fail at solving the equation on the real line. The great thing about Part 2 is
you understand that derivatives related to time can also be made from
spatial derivatives. Of course in practice like physics such systems do not exist, at best it will be some vague 'state space' so this really is a pure math update because choice of the origin in the used coordinate system will change the trajectories.
Enough of this vague bla bla bla,
this update is ten pictures long each size 550 by 1100 pixels.
This is the end of this update, I
hope you learned a bit from it. Let's leave it with that, till updates.
|
|
|
|
|
|