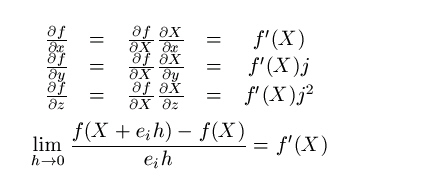|
A primer on the
three dimensional complex numbers.
|
| Introduction: This
file is a collection of the pictures from Feb 2012 until end 2013 that are
related to the 3D complex numbers. 3D complex numbers are in many ways just like the ordinary complex numbers from the complex plane; only in the 3D case you simply 'create' an 'imaginary number' j who's third power equals minus one. Recall that in the ordinary complex plane the 'imaginary unit' i has a square of minus one. Just like ordinary complex numbers (written often as z = x + iy) it looks rather elementary to use rectangular coordinates in real numbers (x, y, z). Therefore the number one is
written as 1 = (1, 0, 0) __________ So only pictures in this stuff below... Remark: Everywhere where in these pictures it says 'see below' you must read that as 'see above' in some other picture. (Because this file is chronological while the homepage of this website is anti-chronological.) |
|
|
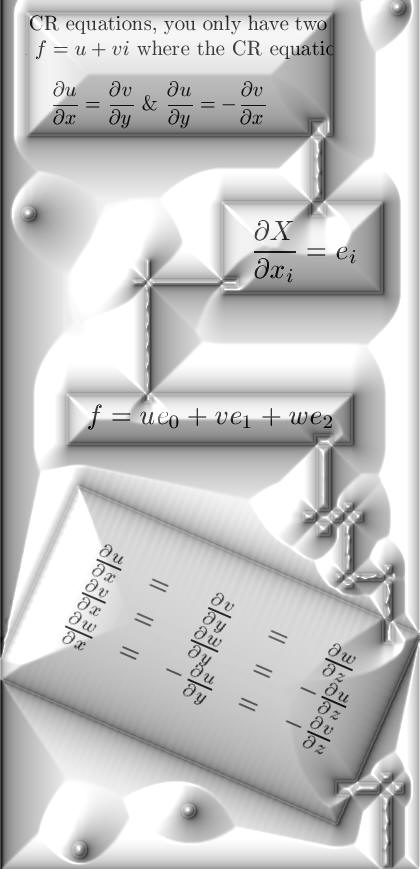
| From 02 Feb last
year a picture under the strange name 'just some math'.
Here you see the generalized Cauchy-Riemann equations for the 3 dimensional case:
|
| From 25 March
2012: This is the 3D complex numbers as a matrix multiplication:
|
| From 12 April 2012:
A little bit more on the matrix representation of a 3D complex number,
remark this picture contains a typo because that D should be the
determinant...
|
| From 28 April 2012:
With help of the matrix representation we calculate the inverse of 3D
complex numbers. Furthermore the conjugate is given; you can see it
behaves a little bit different compared to the flat complex plane.
|
| From 06 July 2012:
In the beginning of July the news of the so called Higgs boson came out,
needless to say that was good news.
So I decided to throw in my 50 cents of help and in the picture below you see the generalized Cauchy-Riemann equations in a much more easy way to understand because the chain rule for differentiation is build within. Ok, at this stadium it is a
bit vague what the capital X is doing in the partial derivates.
: |
| From 09 July 2012:
A very short update was done, in it you see a rather important limit from
the general theory. That explains why it is so important that all your
basis vectors are invertible; otherwise such a limit would be a nonsense
thing...
|
| From 11 Aug 2012:
This was also another important update, you observe how you can simplify
partial differential operators like the Laplacian into differentiation in
only one direction.
|
| From 09 Okt 2012:
This was only a fun update related to austerity troubles in the South of
Europe. May be too much sunny weather is not good for the human mind in
the sense that they start thinking borrowing money is a way of life.
So like the nice gentleman as I am, I wanted to help those countries with savings on universities:
|
| From 03 Dec 2012:
Another glimpse of the general theory; the behavior between the diverse
partial differential operators in a more general space.
And a few properties such transition matrices should have:
|
| From 04 Jan 2013:
The Wirtinger derivates, incomplete version:
|
| From 08 Jan 2013:
After a lot of bullshitting around with the beloved Latex math typesetting
system, there is a more complete version of the Wirtinger derivatives:
|
| From 20 Feb 2013: A
not so serious update, you can see for yourself why it is not that serious
(in the normal world kinetic energy is always a real number and not a
complex number):
|
| From 22 Feb
2013: The same picture about 'kinetic energy' as from 20 Feb 2013, only
now with a background: Much more serious is the update about so called one-forms:
|
| From 12
May 2013: A very simple proof for a very simple statement;
The number i from the ordinary complex plane does not exist in 3 dimensions.
|
| From 21
May 2013: This update is a bit more technical in nature because
it is about differential 2-forms, because it is a bit more technical it is
not published on the homepage but only here.
We calculate a relatively
standard 2-form and relate that via so called 'divisors of zero' to the
Laplacian.
If you never have encountered differential forms, here is a starter from wikipedia: Differential form
|
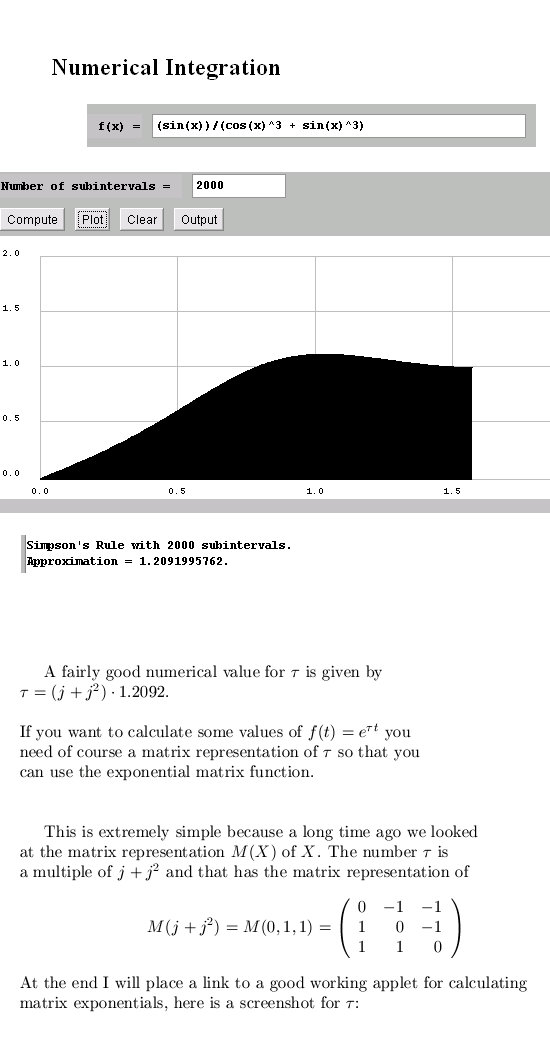
| From 30
May 2013: This update is also rather technical in nature; we
craft a so called Euler identity for the 3-dimensional case, we define the
logarithm and give an integral expression for a very important number
named tau.
I warn you: The five pictures
below contain a whole lot of pure math (and a tiny bit of applied math in
the form of numerical calculus so that we can at least grasp the size of
the number tau). We start with the Euler identity: It is getting a bit more technical in picture number two: Very often if you craft 'good math' the technical difficulties disappear, things get more simple to write down and to understand... Since the integral is a little bit hard to crack, a numerical value for tau is given:
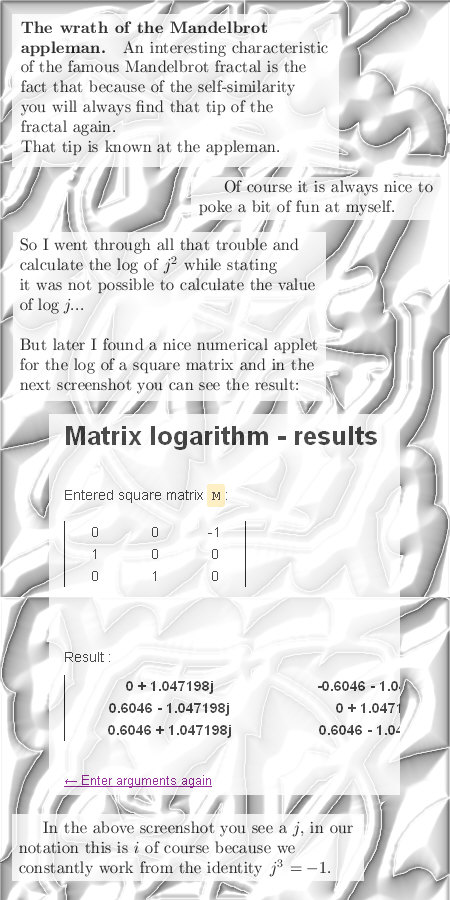
For reasons of completeness I show to you that indeed we have calculated the log of j squared:
The two applets I used, links: http://www.math.tamu.edu/~tkiffe/Fall12/609/Tools/quad.html The numerical evaluation of the integral applet was written by T. Kiffe. http://calculator-fx.com/calculator/linear-algebra/matrix-exponential-using-taylor-series No idea who wrote the matrix exponential applet. __________ And for reasons of being complete, a wiki about the Euler identity in the complex plane: Euler's identity Well that was it for today, till updates.
|
| From 13 June 2013: This
is a possible way of formulating the standard Euler identity for the
ordinary complex plane using the ´tau calculus´ from the previous
update.
Oops: The Euler identities might look the same, of course the number tau in it is different...
|
| From 13
June 2013: In the update from 30 May 2013 we came across a
difficult looking integral that was related to the periodicity of the log
and the exponential in the 3D complex number system. The integral can actually be solved.
Ok ok, I'll be the first one
to admit this proof is rather shaky...
End of the application of massive madness modification, till updates.
|
| From13
July 2013:
Making chopped meat of the 1, 2, 4, 8 theorem.
Again one of the more technical updates, it is not 'very technical' because we only calculate the determinant of a four by four matrix. But it is too technical for the homepage, therefore I place it in this file. My problem with the Hurwitz theorem is that it puts so much emphasis on a norm while as a matter of fact you are only looking at some determinant. The theorem itself is correct but after my humble opinion the importance is far overblown.
Let's leave it with that my dear reader. Till updates.
|
| From 16 July 2013: Oh
oh I should finish that proof that the time exponential of tau is actually
a circle. But I am not one 100% satisfied because the proof still has a little bit of the 'Baron Münchhausen effect' in the sense that I implicit use the fact that it is a circle in order to proof it is a circle... So today we are going to do something different: Poking fun that the results from other people who tried to invent 3-dimensional complex numbers! This is of course a disaster course for making multiplications, but on the other hand it is very charming. And poking fun at myself:
Yeah yeah, Kilroy was here...
Links: A collection of online applets
around linear algebra: http://calculator-fx.com/#linear-algebra How time can ruin your memory!
I would have sworn that 'Kilroy was here' was British, but it seems
to be more or less have an American origin. (Non math): Till updates.
|
| From 31
July 2013: A look at possible matrix representations for slightly
more complicated spaces.
And in the category of 'slightly more technical math' we have a beautiful matrix representing the log of j from our complex 3D numbers:
Nice matrix isn't it? If needed you could use the next nice numerical applet (it uses so called Pade approximation and that works a lot better in the case of the exponential matrix): Matrix exponential using the Pade approximation calculator
|
| From 08
Sept 2013: Ten properties from and related to the exponential tau.
In this update we are going back to the more simple 3-dimensional complex space because there is still a little bit of unfinished work to be done. The first six properties together form a proof that the exponential tau is in fact a circle and this circle lies on the unit sphere. In the last properties we will observe that this circle also is lying on an interesting cone that has it's top in the origin and includes all coordinate axis. Here we go:
We proceed with:
So the above form the proof of the next theorem: The cone stuff is found in the last two properties:
Till updates.
|
| From 23
Sept 2013:
Without comment, some thoughts
on
factorization.
That was it, without comment. Till updates.
|
| From 06
Oct 2013: Again without comment, only some musings on
exponential circles.
Remark that we did not proof
that the third factor is actually a circle... That was it, till updates.
|
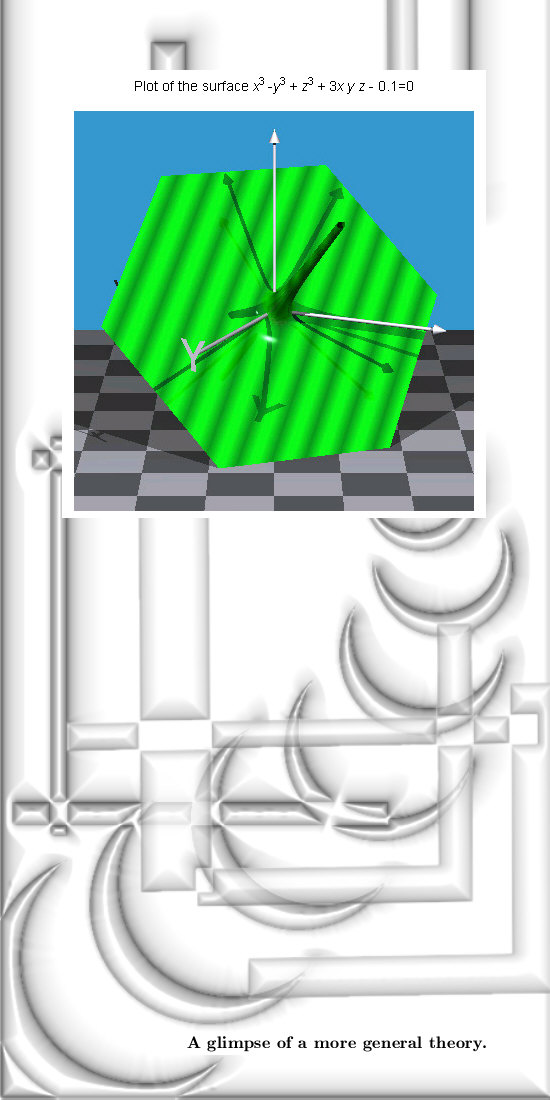
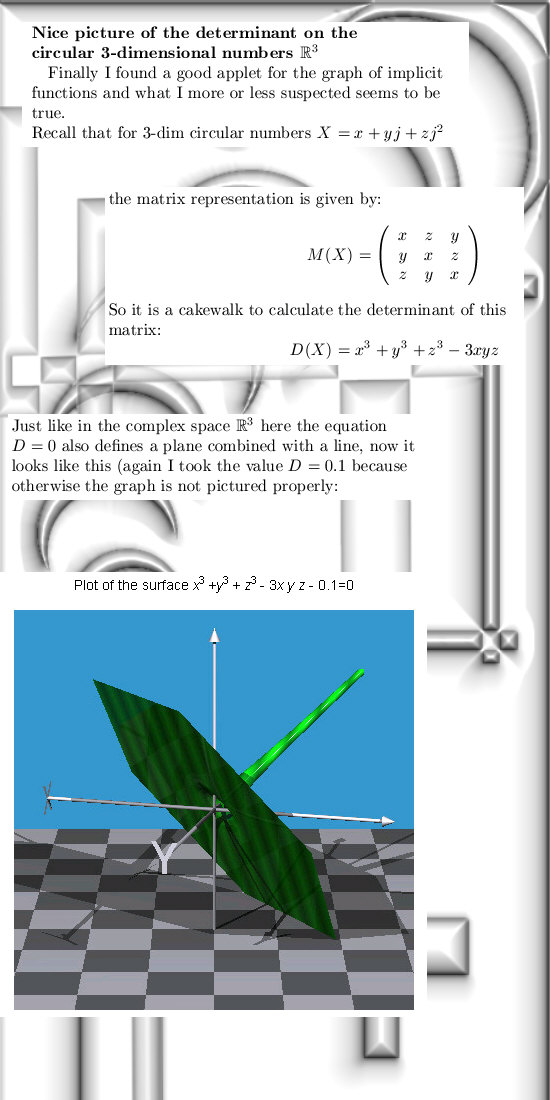
| From 18Oct2013: This
is a long update, we start and end with some graphs upon the determinant
in three dimensions while in between a little bit of the general theory.
As so often general theories are extremely boring, but I hope that if you understand the Sledgehammer theorem you will go through the roof...
At the end we proceed with the determinant in three dimensions, this time with the circular or natural multiplication:
More on circular matrices in, for example, the next wiki: http://en.wikipedia.org/wiki/Circulant_matrix The applet for the two implicit graphs is found in a collection of applets, you have to search a little bit because the direct link to the applet is session bound. But here it is: http://wims.unice.fr/~wims/wims.cgi The name of the applet is polyray (written by XIAO Gang). The applet for the log is of course from this collection of applets: http://calculator-fx.com/calculator/linear-algebra/matrix-logarithm That was it for this update, see you around!
|
| From 01
Nov 2013:
We start with poking a little bit of fun towards the precious professional professors in the algebra, after that we proceed with eigenvalues and eigenvectors for the complex plane and the 3D complex numbers.
Ok, lets hit a button named 'publish website'. Till updates.
|
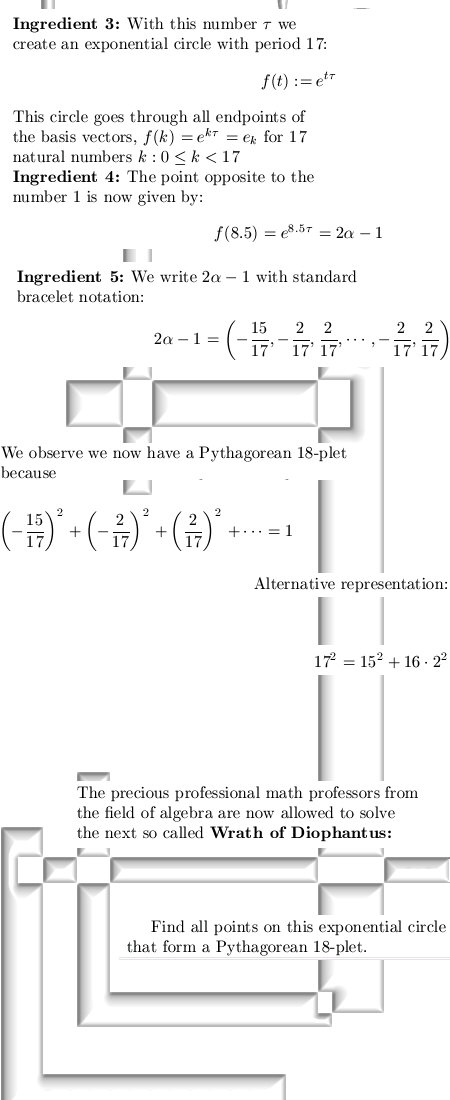
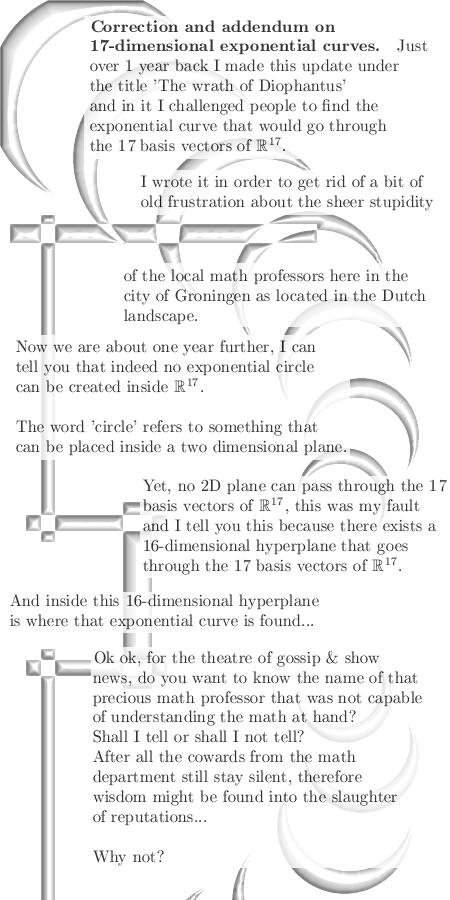
| From 08Nov2013:
This update is by far the most stupid update possible!
Now why is that? Because it contains a very difficult problem, and if you can solve this problem, what have you gained? Nothing... ________ Here we go:
Oh oh, Pythagorean
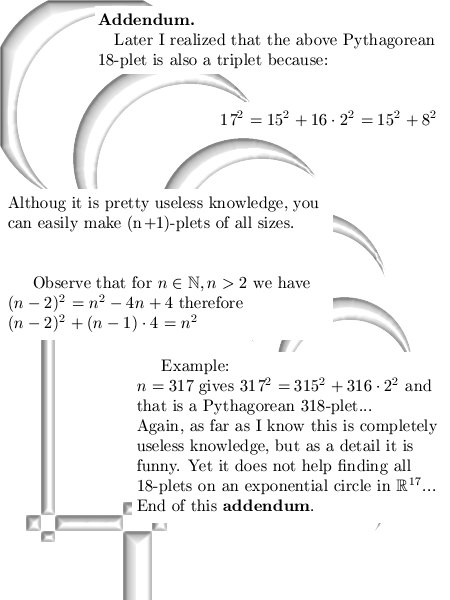
18-plets... Links: In Dutch: __________ Later I added a small addendum with utterly useless knowledge:
Till updates. Addendum
& correction one year later: In higher dimensions it is just not an
exponential circle.
So the name of the precious professor that thought equations of Diophantus were far more important compared to my dumb insights in higher dimensional complex numbers is Marius vd Put. At present date the entire math department still thinks Marius is extremely smart, but I know from experience that Marius was just not capable on only grasping the 3D complex numbers. Let's leave it with that, till updates.
|
| From 28Nov2013: Relations
with linear control theory...
The concepts from linear control theory named controllability and observability are found in all matrix representations we use in our differential algebra's. At the end of the update I do
suggest a possible way of a Fourier transform in three dimensions.
All I can hope for that this
all is not too difficult for our endangered species under the name And in order to understand a little bit how important the concept of controllability is I selected a few Youtubbers about the inverted pendulum. It is amazing how much progress has been made in just the last two decades... From the Technische Uni Wien: Where this is from I don't know, but it is also a must see: __________ A wiki on control theory: State
space representation __________ Till updates.
|
| From 08Dec2013: Correction
(continuous Fourier transform) and addendum (discrete Fourier transform).
In an attempt to get as close as possible to standard math theory, I changed the definition for the continuous Fourier transform a little bit. And for reasons of being complete, after that a few side remarks on the discrete Fourier transform in particular eigenvector/value stuff. Here we go:
Ok, that was it for this update. Till next time. __________ Later updated: You find such matrices of eigenvectors related to the circular multiplication back in strange places, for example what to think of the quantum Fourier transform? Quantum
Fourier transform Do you believe in quantum
computing? Quantum computing is like a dream, there are more of those dreams that will never come to life, for you what is the most realistic dream? You can choose from: -1- Artificial intelligence,
or Till updates.
|
| From 24
Dec 2013: In this update two items:
Item 1) The most general case
for two dimensions, and Item 2 is the 'Song of omega'.
That was it for this update, till the next update.
|
| This file proceeds
on page 2 with 05 Jan 2014, the song of omega reloaded |