|
A primer on the
three dimensional complex numbers.
|
| Introduction: This
file is a collection of the pictures from Feb 2012 until now that are
related to the 3D complex numbers. 3D complex numbers are in many ways just like the ordinary complex numbers from the complex plane; only in the 3D case you simply 'create' an 'imaginary number' j who's third power equals minus one. Recall that in the ordinary complex plane the 'imaginary unit' i has a square of minus one. Just like ordinary complex numbers (written often as z = x + iy) it looks rather elementary to use rectangular coordinates in real numbers (x, y, z). Therefore the number one is
written as 1 = (1, 0, 0) __________ So only pictures in this stuff below... Remark: Everywhere where in these pictures it says 'see below' you must read that as 'see above' in some other picture. (Because this file is chronological while the homepage of this website is anti-chronological.) |
|
|
|
|
| From 05
Jan 2014: This is the second page in these petite investigations in
the higher dimensional complex (and circular) numbers.
Today we are going to look at the roots of unity as found on the exponential circle in the three dimensional complex case. The three dimensional roots of unity are very different compared to the old and known ones from the complex plane; as we will see this is caused by the fact that the center of the exponential circle is not zero but the number alpha... Here is the 3D reloaded stuff, we start with 5 things that are handy to have in your memory/consciousness:
In this update I skipped the
matrices with roots of unity related to the discrete Fourier transform,
very likely they are all non-invertible while in the complex plane these
are unitary matrices... That was it for this update, see you around.
|
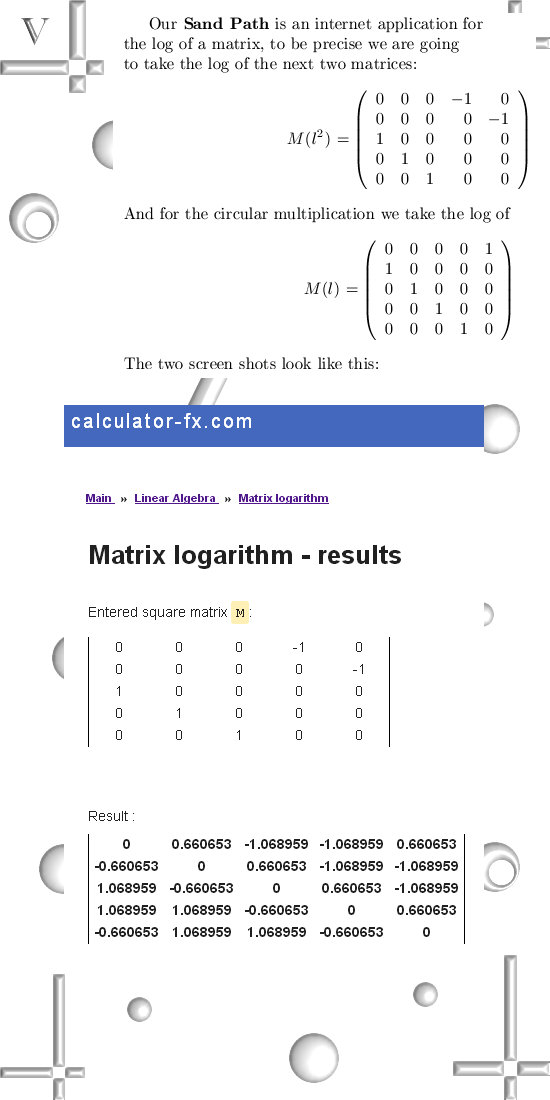
| From 18
Jan 2014: Cauchy integrals.
This update is about double length compared to the size of the usual updates. There is a simple reason for this length: the stuff involved is rather complicated so it takes a lot more trouble to explain everything properly. Let' s not waste time and put
your brains to work!
Updated 26 March 2016: I corrected the above matrix for the log of -j, circular multiplication. I am sorry it took me so long to remark the fault there was within. Well this is directly related to the fact my work is never peer checked, that is good for the quantity but at the same time I cannot guarantee it is always flawless...
In case you have never seen a Cauchy integral, a relative good youtubber is made by doctorphys (the video contains a small fault but all in all it explains the complex plane relatively good):
Wikipedia has a nice collection that contains both the resolvent and the spectrum mapping theorem: Holomorphic
functional calculus __________ Ok, that was it for this time. Till updates.
|
|
From 30 Jan 2014: The 5D complex numbers and the golden ratio. This is another 10 page long update and
I ask myself as why am I doing this? __________ Ok, after having said that, on 22 Feb I
replaced a few things because of typo´s, better formulae format and most
of all: in 5D these are not exponential circles but exponential
curves. Let us look at the stuff from this improved 22 Feb update:
Not related very much to the above, but a Popular Science outlet named the New Scientist has a funny file that says two dimensional complex numbers can be harmful if they do not fit... From
i to u: Searching for the quantum master bit Let' s leave it with that.
|
| From 03
March 2014: A simple model for the proton and the neutron.
Further reading: The
Standard Model Till updates.
|
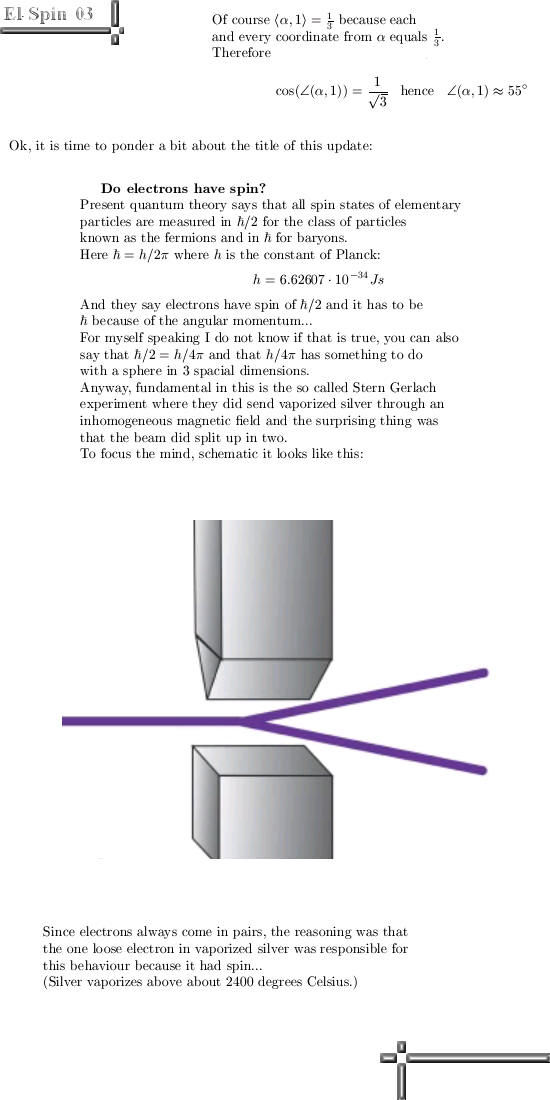
| From 29
April 2014 : Do electrons have spin?
For myself speaking I do not
believe electrons have spin since they behave a lot like magnetic
monopoles. So be it, but in this update
it is a bit more about how I look at the spin stuff.
My dear reader, what do you think? Do electrons have spin and are they standard magnetic dipoles with a north and a south pole? In the science of chemical things, they say electrons only come in pairs but if they were magnetic dipoles also 4, 6, 8 etc configurations would be allowed. Since we only observe pair like behavior logic says that electrons might very well be magnetic monopoles... Till updates. Update from 02 May: At the end of the Feynman lectures on physics you can observe all kinds of interesting thingelings like the original Stern-Gernbach experiment from the year 1922. But for myself speaking I observe the honorable Richard Feynman stating stuff like that it is impossible for the electron spin to be exactly measured into the z-axis direction... Again: Standard quantum theory does not say why the z-axis would be special in any way. But if you see it as the
direction of the alpha axis in 3-dimensional complex numbers, suddenly the
stuff makes a lot more sense. After all alpha is a non-invertible number
and although I never mentioned it, alpha also plays a crucial role in the
wave equation. Update from 08 May: Not much important or complicated but those spin half numbers have a strange property. Till updates.
|
|
From 28 May 2014: This update contains no math at all. In this update I first tried to find some counter examples against electrons being magnetic monopoles, yet everything found points into the direction that electrons are magnetic monopoles.
The 'wrong picture' is from a Youtubber with the title From
Atoms to X-rays The energy splitting picture is from Electron
Paramagnetic Resonance: Theory And I don't remember where I got the Zeeman effect picture from. __________ A guy named Paul Callaghan
presents a nice series on MRI where all the basics are covered in a Introductory
NMR & MRI Also important is
understanding the so called rare earth metals, they are known as the
Lanthanide Series in the periodic system of chemical elements. The
importance lies in the fact they all have only 2 electrons in their most
outer orbital but inside they have lots of unpaired electrons. The
Lanthanide Series __________ Till updates.
|
|
From 02 Aug 2014: The outer product in 3D. This update is five pictures, or equivalent, five A4 size pages long but most stuff is repeating from previous updates. The only new thing is the outer product. Does that mean I do not have new things? No, I have plenty of new things but lately I arrived at the conclusion that apparently no university and no department of mathematics is waiting for this. There is only this wall of silence and so I wondered as why I should let insult myself by a bunch of incompetent people? Not only incompetent from the
professional point of view, after all century in century out they could
not find the higher dimensional complex numbers; but also that
incompetence on the emotional level. Ok, here we go:
That was it for this update, Till updates.
|
| From 15
Sept 2014: The superposition of quantum states using 3D circular numbers from the 3D exponential circle. Important remark: Since my
knowledge of quantum mechanics is rather limited, I decided to use the
three colors of quarks as the three states that are supposedly to be in a
'superposition'. I take no responsibility for the Quantum Mechanics used, I take only responsibility for the math parts used like higher dimensional complex and circular numbers. To be precise: circular numbers from our 3D world... End of this remark. __________ Six pictures will paint what I had to say on this subject, here we go:
Embargo information: __________ Useful links: From MIT OpenCourseWare an intro in superposition of quantum states, it's a Youtube video: Introduction
to superposition And as usual I made the
picture about the determinant with an applet under the name of Polyray. So search for Polyray: WIMS
End of this update.
|
| From 26
Nov 2014: An overview of 10 exponential circles & curves;
back in the year 1748 a guy named Leonhard Euler found the very first
exponential circle. It is the unit circle around the origin in the complex
plane. The very first exponential circle goes under a lot of names, but if
you write down the two words 'Euler identity' most readers understand you
are writing about the unit circle in the complex plane.
As far as I know, during a
period of 260 years no other folks have found more exponential circles. The reason for that is very
simple, let me give you a simple example like for the five dimensional
real vector space: The exponential curve will go through all five basis
vectors but it is not possible for a two dimensional plane to go through
all five basis vectors... (Ok ok, that is not 100% true, but for the circular version of multiplication of 5D complex numbers it is. For the complex version in 5D space, sometimes not the positive basis vector but the minus of that basis vector is in the path of the exponential curve.) For myself speaking, I consider the finding of all these exponential circles and curves as definitely inside the top 10 of mathematical results found during my entire life. It is not very often that you can improve on an important result in math that is the blood and veins of complex analysis. __________ Ok, let's hit the road; Here
are 20 pages with the description of 10 exponential circles and curves.
And now you are at the end of
this 19 pages long update on 10 new exponential circles and curves. On page 20 just some pictures where I try to visualize the 3D exponential circle a little bit:
Usefull links: For the matrix exponential and the log of a matrix you can go to: http://calculator.vhex.net/function-index/linear-algebra The visualization pictures for
the 3D exponential circle come from an applet named polyray. http://wims.unice.fr/~wims/wims.cgi Till updates.
|
| From 16
Dec 2014: What did Hamilton do wrong in 3D?
A lot of the so called
'professional math professors' seem to think that 3-dimensional complex
numbers do not exist because for example that Irish guy named Hamilton
could not find them. In this update I explain what
Hamilton did do wrong; the most important detail is the fixation on the
Euclidean norm that he thought had to be preserved under
multiplication. This update is short, just 3
pages.
Source file: Liberation_Of_Algebra_part1.avi Till updates.
|
| From xx xxx 2015: |
|
From xx xxx 2015: |
|
|
|
|